论文简析
原论文:FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
研究背景
Transformer 模型在自然语言处理和图像分类等领域被广泛应用,但其核心的自注意力模块在处理长序列时面临时间和内存复杂度呈二次方增长的问题,限制了模型对更长上下文的处理能力。尽管已有许多近似注意力方法试图通过降低计算复杂度来解决这一问题,但这些方法往往未能显著提升实际运行速度,且可能牺牲模型性能。
新方法
本文提出了一种新的注意力算法 FLASHATTENTION,旨在通过减少 GPU 内存访问次数(即 I/O )来显著提高 Transformer 模型在长序列上的运行速度和内存效率,同时保持注意力计算的精确性。
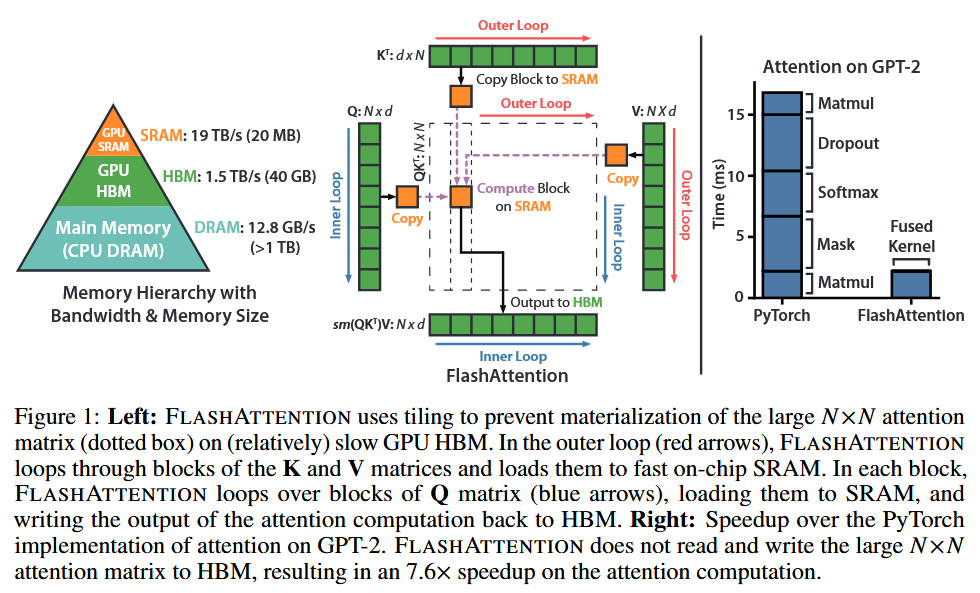
FLASHATTENTION 方法:
- 分块(Tiling):将输入矩阵 Q、K、V 分成小块,逐块加载到 GPU 的快速片上 SRAM 中进行计算,避免一次性将整个大矩阵加载到较慢的 HBM 中。
- 重计算(Recomputation):在反向传播中,通过存储前向传播中的 softmax 归一化因子,利用这些因子在 SRAM 中快速重新计算注意力矩阵,而不是从 HBM 中读取中间结果,从而减少 HBM 访问次数。
- 融合操作(Kernel Fusion):将所有注意力操作融合到一个 GPU 内核中,避免多次从 HBM 读取输入和写入输出,进一步减少内存访问开销。
- 扩展到稀疏注意力:进一步将 FLASHATTENTION 扩展为块稀疏版本,通过仅计算非零块的注意力矩阵,进一步降低内存访问次数和计算复杂度。
总结
本文提出了 FLASHATTENTION,一种针对 Transformer 模型的高效精确注意力算法。通过分块、重计算和融合操作,FLASHATTENTION 显著减少了 GPU 内存访问次数,从而在长序列上实现了更快的训练速度和更低的内存占用。实验表明,该方法不仅加速了模型训练,还通过扩展上下文长度提高了模型性能,为 Transformer 模型在长序列任务中的应用提供了新的可能性。
标准 Attention

其中$Q, K, V$ 都是形状为 $(N\times d)$ 的矩阵, $S, P$ 是形状为 $(N\times N)$ 的矩阵。
从而可知:
- 如果要在只读写一次 HBM 的情况下完成整个计算,SRAM 中至少需要 $O(Nd+N^2)$ 的空间(保存QKV,注意力矩阵以及中间计算结果),但在实际应用中序列长度 $N$ 通常非常大,导致显存需求远超 SRAM 容量。
- 所以在标准 Attention 的计算中,需要频繁地访问 HBM 以获取计算数据,I/O 需求为 $O(Nd+N^2)$ ,与序列长度的平方相关。
一般来说,一个程序的执行速度瓶颈有两类:计算瓶颈与内存瓶颈。而在标准 Attention 中,计算效率的瓶颈正是频繁的显存访问(HBM I/O)。
分块 Softmax 计算
在正式开始介绍 FlashAttention 之前,需要先了解 Softmax。因为在其分块计算的过程中,最为复杂的就是如何分块计算 Softmax 。
Softmax
Softmax 函数是机器学习和深度学习中广泛使用的归一化指数函数,主要用于将任意实数向量转换为概率分布,其计算公式如下:
$$\text{Softmax}(x_i)=\frac{e^{x_i}}{\sum^{n}_{j}e^{x^j}}$$
其中:
- 对输入进行指数变换,以放大元素间差异。
- 分母为归一化因子,以确保输出的所有元素和为 1。
Safe Softmax (3-Pass)
在计算 Softmax 时,即使数据类型为 FP32,当 $x_i=89$ 时,分子$e^{x_i}$ 已经超过了 FP32 的范围。Safe Softmax 通过减去$x_i$中的最大值,来避免数据溢出,其公式如下:
$$\text{Safe-Softmax}(x_i)=\frac{e^{x_i-m}}{\sum^{n}_{j}e^{x_j-m}}, m=\max(x_1,x_2,\ldots,x_n)$$
因为 $x_i-m\le 0$ ,所以避免了分子数据溢出。
python 简单实现如下:
# Safe Softmax (3 Pass)
import math
def safe_softmax_3pass(x):
# 找到全局最大值 m
m = float('-inf')
for i in range(len(x)):
m = max(m, x[i])
# 计算分母归一化指数的和 d
d = 0
for i in range(len(x)):
d += math.exp(x[i] - m)
# 计算 softmax 的值
a = [0 for _ in range(len(x))]
for i in range(len(x)):
a[i] = (math.exp(x[i] - m) / d)
return a当输入为 [1, 2, 3, 4] 时,输出为:
output = safe_softmax_3pass([1, 2, 3, 4])
print(f"Output:{output}")
# Output:[0.03205860328008499, 0.08714431874203257, 0.23688281808991013, 0.6439142598879724]不难看出,整个计算需要经过三次遍历。且若没有足够的 SRAM 的空间存下所有数据,则每次遍历都需要从 HBM 中读取相应数据,增加 I/O 访问。
Safe Softmax (2-Pass)
通过合并前两步的计算,可以减少遍历次数,从而加快计算速度。
第一次遍历 ($i: 1 \rightarrow N$):
$$m_i = \max(m_{i – 1}, x_i)$$
$$d_i = d_{i-1}\cdot e^{m_{i-1}-m_i}+e^{x_i-m_i}$$
第二次遍历 ($i: 1 \rightarrow N$):
$$a_i=\frac{e^{x_i-m_N}}{d_N}$$
证明如下:
- 若 $x_i\le m_{i-1}$,即前 $i$ 项的最大值没有变化,$m_i = m_{i-1}$,所以 $d_i$ 只需要加上第 $i$ 项的归一化指数
- 若 $x_i\gt m_{i-1}$,即第 $i$ 项才是当前最大值,$m_i=x_i$,所以前 $i-1$ 项的归一化指数的计算需要更新,需要由 $e^{x_j-m_{i-1}}$ 更新为 $e^{x_j-m_i}$,即指数需要多减去差值$m_i-m_{i-1}$
- $$d_{i-1}’=d_{i-1}\cdot e^{-(m_i-m_{i-1})}=d_{i-1}\cdot e^{m_{i-1}-m_i}$$
- $$d_i = d_{i-1}’+e^{x_i-m_i}=d_{i-1}\cdot e^{m_{i-1}-m_i}+e^{x_i-m_i}$$
python 代码如下:
# Safe Softmax (2 Pass)
import math
def safe_softmax_2pass(x):
# 每次更新最大值与分母归一化指数项的和
m = float('-inf')
d = 0
for i in range(len(x)):
m_new = max(m, x[i])
d = d * math.exp(m - m_new) + math.exp(x[i] - m_new)
m = m_new
# 计算 softmax 的值
a = [0 for _ in range(len(x))]
for i in range(len(x)):
a[i] = math.exp(x[i] - m) / d
return a当输入为 [1, 2, 3, 4] 时,输出为
output = safe_softmax_2pass([1, 2, 3, 4])
print(f"Output:{output}")
# Output:[0.03205860328008499, 0.08714431874203257, 0.23688281808991013, 0.6439142598879724]结果与上一节的 3-pass 一致。
分块 Softmax
FlashAttention 算法中分块 Softmax 的计算思路与 Safe Softmax (2-Pass) 是一致的,只是更新的频率从每一项变成了每一块。
- 计算第 $i$ 块的局部最大值 $\tilde{m}_{ij}$,并根据该局部最大值求得每一项的归一化指数和 $\tilde{\ell}_{ij}$。
- 计算前 $i$ 块的最大值 $m_i^{\mathrm{new}}=\max(m_i,\tilde{m}_{ij})$。
- 更新前 $i$ 块的归一化指数和(与 2-Pass 的思路一致) 。
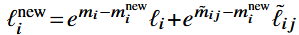
FlashAttention

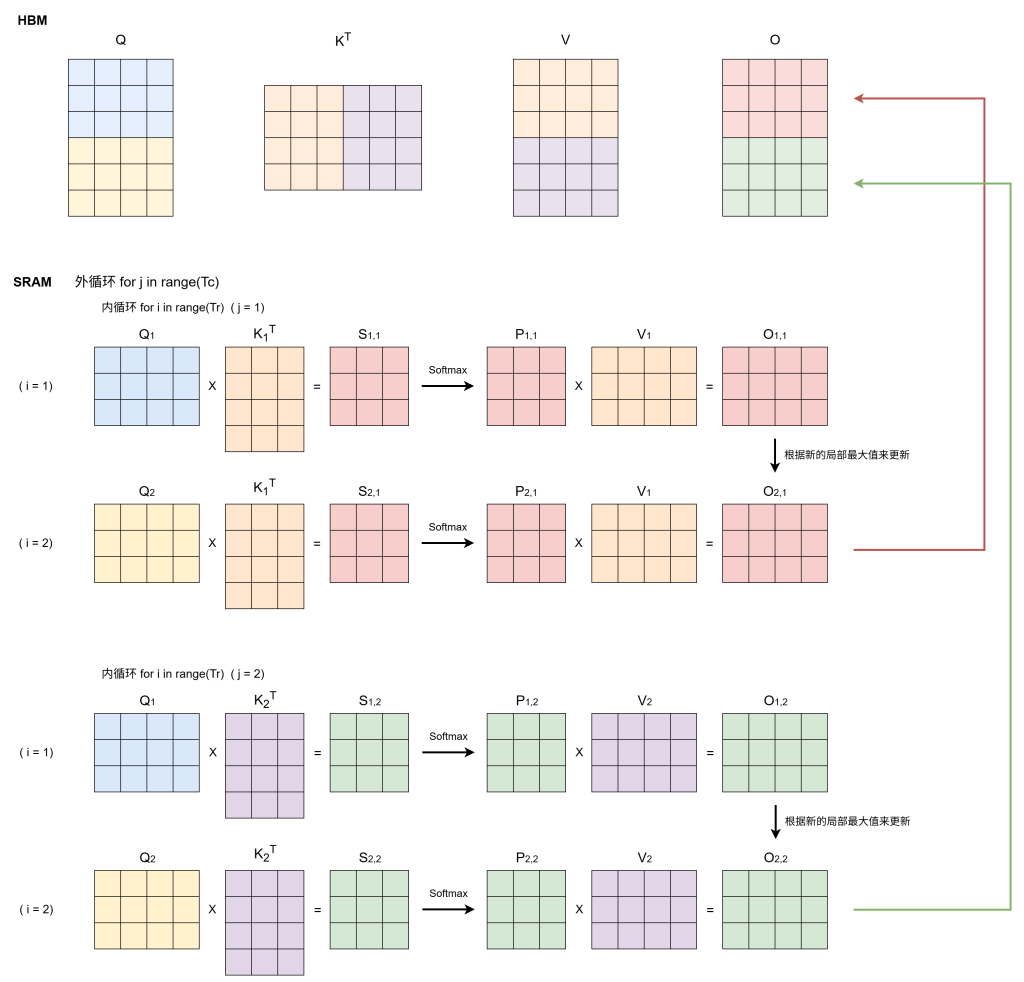
分块(step 1-4)
假设 $\mathbf{Q},\mathbf{K},\mathbf{V}\in\mathbb{R}^{N\times d}$ 在 HBM 上。
step 1 确定分块大小
$B_{c}=\lceil\frac{M}{4d}\rceil$ :$B_{c}$ 是 $\mathbf{K},\mathbf{V}$ 的列分块大小。向上取整是为了分更多的块,从而确保 SRAM 能同时存下计算所需的数据。$M$ 是 SRAM 的大小,除以 $4d$ 是因为需要同时存放 $\mathbf{Q},\mathbf{K},\mathbf{V},\mathbf{O}$。
$B_{r}=\min(\lceil\frac{M}{4d}\rceil,d)$:$B_{r}$ 是 $\mathbf{Q}$ 的行分块大小,并限制不超过 $d$,这可以保证分块后的 $\mathbf{Q}_i$ 在计算时能够存放中间计算结果 $\mathbf{S}_ij$。
step 2 预留结果暂存空间
$\mathbf{O}$ 是最后的输出,$\ell$ 是计算 Softmax 时的归一化指数和, $m$ 是每一块以及之前块的最大值。
step 3-4 将矩阵分块
$T_c$ 为 $\mathbf{K},\mathbf{V}$ 的分块数量。
$T_r$ 为 $\mathbf{Q}$ 的分块数量,同时也是 $\mathbf{O},\ell,m$ 的分块数量。
双循环计算(step 5-15)
内循环
$\mathbf{Q}_1\rightarrow \mathbf{Q}_{T_r}$:每次加载新的 $\mathbf{Q}_i$,而$\mathbf{K}_j,\mathbf{V}_j$ 不变。
- 计算注意力分数$\mathbf{S}{ij}$(step 9)
- 分块 softmax,前面已经讲过 (step 10-11)
- 更新 $\mathbf{O}_i$(step 12):这里前一项可以写成 $(\ell_i\mathbf{O}_i)\frac{e^{m_i-m_i^{new}}}{\ell_i^{new}}$,即先将前 $i-1$ 块的和还原,再重新计算新的结果,然后再加上第 $i$ 块的结果
- 更新 $\ell_i,m_i$ (step 13)
外循环
$\mathbf{K}_1,\mathbf{V}_1\rightarrow \mathbf{K}_{T_c},\mathbf{V}_{T_c}$:加载新的 $\mathbf{K}_j,\mathbf{V}_j$,并再次遍历 $\mathbf{Q}$ 的每一块进行计算
示意图
代码实现
# 手动实现 FlashAttention 的计算,不涉及反向传播
import torch
import math
# 论文中 QKV 的形状为 (N, d),对应到这里为 (seq_len, head_dim)
def my_flash_attention(query, key, value, mask=None):
# 负无穷大
neg_inf = float('-inf')
# epsilon 防止除零
epsilon = 1e-6
# N,d
seq_len = query.size(-2)
head_dim = query.size(-1)
# 预留 output
output = torch.zeros_like(query, device=query.device, dtype=torch.float16)
# 记录分块 softmax 中的最大值
m = torch.ones(query.shape[:-1], device=query.device, dtype=torch.float16)[..., None] * neg_inf
# 记录分块 softmax 中的和
l = torch.zeros(query.shape[:-1], device=query.device, dtype=torch.float16)[..., None]
# KV 的列分块大小,论文中由 M 决定,此处暂取为固定值
B_c = 4
# Q 的行分块大小
B_r = min(B_c, head_dim)
# KV 的分块数量
T_c = math.ceil(seq_len / B_c)
# Q 的分块数量
T_r = math.ceil(seq_len / B_r)
# 将 QKV 分块
query_blocks = torch.split(query, B_r, dim=-2)
key_blocks = torch.split(key, B_c, dim=-2)
value_blocks = torch.split(value, B_c, dim=-2)
# mask分块
mask_blocks = list(torch.split(mask, B_c, dim=-1))
# 将 output、m、l分块
ouput_blocks = list(torch.split(output, B_r, dim=-2))
m_blocks = list(torch.split(m, B_r, dim=-2))
l_blocks = list(torch.split(l, B_r, dim=-2))
# 分块计算注意力
# 外循环:j -> T_c
for j in range(T_c):
key_j = key_blocks[j]
value_j = value_blocks[j]
mask_j = mask_blocks[j]
# 内循环:i -> T_r
for i in range(T_r):
query_i = query_blocks[i]
output_i = ouput_blocks[i]
m_i = m_blocks[i]
l_i = l_blocks[i]
# 计算 Q@K^T/sqrt(d_k)
S_ij = torch.matmul(query_i, key_j.transpose(-2, -1)) / (head_dim ** 0.5)
# mask
if mask_j is not None:
S_ij = S_ij.masked_fill(mask_j.unsqueeze(1) == 0, float('-inf'))
# 分块 softmax
m_ij, _ = torch.max(S_ij, dim=-1, keepdim=True)
P_ij = torch.exp(S_ij - m_ij)
l_ij = torch.sum(P_ij, dim=-1, keepdim=True) + epsilon
# 更新最大值
m_i_new = torch.max(m_i, m_ij)
l_i_new = torch.exp(m_i - m_i_new) * l_i + torch.exp(m_ij - m_i_new) * l_ij
# 计算并更新 output
ouput_blocks[i] = (l_i * torch.exp(m_i - m_i_new) * output_i + torch.exp(m_ij - m_i_new) * torch.matmul(P_ij, value_j)) / l_i_new
# 更新 m、l
m_blocks[i] = m_i_new
l_blocks[i] = l_i_new
# 拼接 output
output = torch.cat(ouput_blocks, dim=-2)
# 拼接 m、l
m = torch.cat(m_blocks, dim=-2)
l = torch.cat(l_blocks, dim=-2)
return output结果验证
参考值
生成随机的 Q,K,V
import math
import torch
import torch.nn as nn
from torch.nn import functional as F
from torch.nn.attention import sdpa_kernel, SDPBackend
# 设置随机种子
torch.manual_seed(1)
# 定义输入参数
batch_size = 1
seq_len = 10
embed_dim = 6
num_heads = 2
head_dim = embed_dim // num_heads
# 随机生成输入张量 (batch_size, num_heads, seq_len, head_dim)
query = torch.randn(batch_size, num_heads, seq_len, head_dim, device='cuda', dtype=torch.float16)
key = torch.randn(batch_size, num_heads, seq_len, head_dim, device='cuda', dtype=torch.float16)
value = torch.randn(batch_size, num_heads, seq_len, head_dim, device='cuda', dtype=torch.float16)
# 随机生成注意力掩码 (batch_size, seq_len)
mask = torch.randint(0, 2, (batch_size, seq_len), device='cuda', dtype=torch.float16)在 PyTorch 中有一个函数为 scaled_dot_product_attention,它有三种实现方式
- FlashAttention
- 标准数学实现
- 内存高效注意力
标准数学实现
在这里,我们通过上下文控制器来调用其 FlashAttention 与标准数学实现
# 标准数学实现
with sdpa_kernel(SDPBackend.MATH):
output_pytorch_flash = F.scaled_dot_product_attention(
query, key, value,
attn_mask=None,
dropout_p=0.0,
is_causal=False
)
# Output: (batch_size, num_heads, seq_len, head_dim)
print(f"Shape:{output_pytorch_flash.shape}")
print(output_pytorch_flash)标准数学实现输出结果
Shape:torch.Size([1, 2, 10, 3])
tensor([[[[ 0.4641, 0.1559, -0.4280],
[ 0.1121, 0.3057, -0.1246],
[ 0.3330, 0.3147, -0.0417],
[-0.0228, 0.7021, -0.0097],
[ 0.0540, 0.2869, 0.1398],
[-0.0387, 0.5156, -0.0123],
[-0.0682, 0.3875, 0.1809],
[-0.1488, 0.4080, -0.0170],
[-0.3777, 0.6719, -0.4998],
[-0.0193, 0.1809, -0.5254]],
[[-0.4082, -0.4016, 0.2546],
[ 0.2925, 0.4536, 0.2051],
[-0.2620, 0.0322, -0.1362],
[-0.3171, 0.0995, -0.1333],
[-0.5464, -0.6416, 0.4722],
[-0.4858, -0.4067, 0.2091],
[-0.2115, -0.0323, -0.0919],
[-0.1204, 0.1034, 0.1997],
[ 0.0822, 0.3242, -0.2644],
[-0.0407, 0.1741, -0.1674]]]], device='cuda:0', dtype=torch.float16)PyTorch 的 FlashAttention 实现
# FlashAttention实现
with sdpa_kernel(SDPBackend.FLASH_ATTENTION):
output_pytorch_flash = F.scaled_dot_product_attention(
query, key, value,
attn_mask=None,
dropout_p=0.0,
is_causal=False
)
# Output: (batch_size, num_heads, seq_len, head_dim)
print(f"Shape:{output_pytorch_flash.shape}")
print(output_pytorch_flash)计算结果
Shape:torch.Size([1, 2, 10, 3])
tensor([[[[ 0.4641, 0.1558, -0.4280],
[ 0.1121, 0.3059, -0.1246],
[ 0.3330, 0.3147, -0.0417],
[-0.0228, 0.7021, -0.0098],
[ 0.0540, 0.2866, 0.1398],
[-0.0386, 0.5156, -0.0124],
[-0.0682, 0.3875, 0.1809],
[-0.1487, 0.4080, -0.0170],
[-0.3777, 0.6724, -0.4998],
[-0.0193, 0.1810, -0.5254]],
[[-0.4082, -0.4016, 0.2546],
[ 0.2925, 0.4539, 0.2051],
[-0.2620, 0.0322, -0.1361],
[-0.3171, 0.0995, -0.1333],
[-0.5464, -0.6416, 0.4722],
[-0.4858, -0.4067, 0.2091],
[-0.2115, -0.0323, -0.0918],
[-0.1204, 0.1035, 0.1997],
[ 0.0822, 0.3242, -0.2644],
[-0.0407, 0.1741, -0.1674]]]], device='cuda:0', dtype=torch.float16)FlashAttention 计算结果
Shape:torch.Size([1, 2, 10, 3])
tensor([[[[ 0.4641, 0.1556, -0.4280],
[ 0.1121, 0.3057, -0.1247],
[ 0.3330, 0.3147, -0.0420],
[-0.0229, 0.7017, -0.0099],
[ 0.0542, 0.2866, 0.1396],
[-0.0385, 0.5156, -0.0123],
[-0.0681, 0.3870, 0.1810],
[-0.1488, 0.4084, -0.0168],
[-0.3765, 0.6719, -0.5000],
[-0.0194, 0.1809, -0.5254]],
[[-0.4080, -0.4019, 0.2554],
[ 0.2925, 0.4536, 0.2053],
[-0.2620, 0.0321, -0.1362],
[-0.3171, 0.0994, -0.1332],
[-0.5464, -0.6421, 0.4727],
[-0.4856, -0.4067, 0.2091],
[-0.2118, -0.0326, -0.0917],
[-0.1205, 0.1035, 0.1996],
[ 0.0822, 0.3240, -0.2644],
[-0.0406, 0.1741, -0.1674]]]], device='cuda:0', dtype=torch.float16)经过对比可以发现计算结果与参考值一致,误差可接受。
加入 mask 的计算结果与自己实现的 Attention 计算的结果是一致的,而 scaled_dot_product_attention 的标准数学实现在引入 mask 之后结果并没发生改变,同时其 FlashAttention 实现并不支持 mask 为非空的计算。这一点暂不理解。
Todo
- 目前正在尝试实现cuda版本的FlashAttention